First of all: The videos you posted above look really interesting! I’m not really deeply into the theory behind what you are doing there, but just a few points that might be worth thinking about and which may help you understanding the whole topic
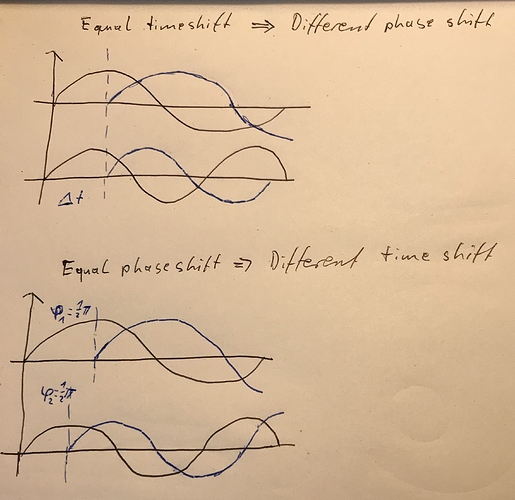
Phase shift vs. time shift
If you take a pure single frequency sine wave and create a time shifted version of that wave you can express the shift amount either in e.g. seconds if it is a time based signal, in samples if it is a sampled signal (which will in the end equal a time shift in discrete time steps, depending on your sample rate, so this should just be listed under time shift in the following part) or as a phase shift. All three are explanations of the same effect. While the time shift is an absolute value in seconds, the phase shift is a relative value , in detail a fraction of the wave-length multiplied by 2pi or 360° (lets stick to radians here).
Now if we take two sine waves with different frequency, played at the same time and apply a constant time shift to it, this will result in a different phase shift for both, as both waves differ in their wavelength. On the other hand, if we apply the same phase shift to both, it will result in a different time shift for both. I tried to quickly draw that to explain what I mean 
:
What does phase shifting a whole signal mean?
So with this knowledge, what does phase shifting a complete signal mean? As Mr. Fourier found out nearly 200 years ago (an amazing fact, by the way), all time signals can be decomposed into and fully described by a number of sine waves that represent each frequency occurring in the signal, the complete signal equals the sum of all those sines. A fourier transform computes the magnitude and phase of all the sine waves needed to create the signal you put into it.
Now if we try to think of our signal as a big number of sine waves with different frequencies and look at the drawing above, this would mean an individual time shift of each of this frequencies in order to obtain a constant phase shift for all frequencies. A simple time shift of the overall signal wouldn’t do.
So which kind of tool is needed to perform that operation?
Short answer: An allpass filter with a constant phase shift.
A short introduction to filters
As you might know, a filter is some abstract kind of processing block that alters the magnitude of the incoming signal over the frequency and introduces a phase shift over the frequency. In case of an EQ, the phase shift is not so important in many cases, as it is not directly audible if you listen to the output signal alone. If this is the case, we normally use super efficient IIR filter structures, they alter the magnitude and you have to deal with the phase shift. We can also create linear phase equalizers with FIR filters, they are computationally more heavy but can achieve an arbitrary magnitude combined with a linear phase. And we can create all pass filters. They have a linear magnitude and only introduce a phase shift.
How to build that allpass?
If you want a true linear magnitude combined with a phase shift equal for all frequencies, you need an FIR filter. An IIR biquad-based allpass is not suitable for this case of constant phase shift over all frequencies. While a true constant phase shift is not so hard to achieve with an FIR filter, a true linear magnitude is only achieved by a longer filter, which will be computationally more expensive.
The FFT-based solution
A straightforward solution is what you have done in max: Computing the FFT, shifting the frequencies of the resulting spectrum and don’t touch the magnitude. In fact, mathematically this can be seen as a way to implement an FIR based allpass, you basically perform a convolution here. However, if you want to go that route, you should have a look at how convolution is done right, because you will need to compute some kind of overlap and add it to the next block – otherwise you will introduce (subtle) artifacts to your output signal.
The FIR-based solution
All this can done with an FIR filter as well, completely without an FFT. With filter design tools as found in Matlab etc. you can compute the corresponding filter coefficient to create any FIR filter that does anything to your phase. However if you want to change the phase shift at runtime, re-computing can or cannot be a computationally heavy task.
Now what’s with the Hilbert filter
Ah right. The Hilbert filter. This thing is a bit difficult to understand, as it basically creates a complex-valued version of your real-valued input signal. While the spectrum of a real-valued signal is symmetric for negative frequencies (and therefore is not computed and displayed at all most of the time when working with real valued audio signals), the spectrum of a Hilbert filtered signal is zero for negative frequencies 
You can even reduce the sample rate after hilbert filtering down to 1/2 without any aliasing effects, but this is another topic…
The hilbert filter basically creates a signal with +1/2 pi phase shift for positive frequencies and -1/2pi phase shift for negative frequencies, a so-called IQ signal (In phase and Quadrature). By applying gain to the I or Q part of the signal, you can now create an arbitrary phase shift to the signal. To get back a real valued signal, just sum both parts up. If you want to compute an FFT on such a signal, just chose a complex to complex FFT.
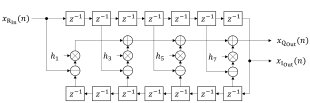
That being said, I only did a hilbert filter for non-audio applications so far. Here is a figure from my master thesis where I described the filter structure that I implemented
I chosed to implement it with only 15 coefficients and you see that the resulting magnitude is far from being constant – however it was sufficient for my use case back then. Another interesting thing is the repeating coefficient pattern – this can be exploited to reduce the computational complexity of such a structure quite a bit:
But those are implementation details 
I hope this could at least shed some light at some of the aspects and give you an idea what to google for
Edit: Why do my uploaded pictures look so bad here?