IIRCoefficients gain for peak filter bug

General JUCE discussion
1

Hi,

I just found out when you pass 0 gainFactor to the IIRCoefficients::makePeakFilter the fifth coefficient is nan. Reason:

In the IIRCoefficients::makePeakFilter the A is zero and is used as denominator for the alphaOverA which is then infinite.

const double A = jmax (0.0f, std::sqrt (gainFactor));
const double omega = (double_Pi * 2.0 * jmax (frequency, 2.0)) / sampleRate;
const double alpha = 0.5 * std::sin (omega) / Q;
const double c2 = -2.0 * std::cos (omega);
const double alphaTimesA = alpha * A;
const double alphaOverA = alpha / A;

This values are passed to constructor of IIRCoefficients like this:

return IIRCoefficients (1.0 + alphaTimesA,
                        c2,
                        1.0 - alphaTimesA,
                        1.0 + alphaOverA,
                        c2,
                        1.0 - alphaOverA);

And in the constructor itself you can see the problem. The c4 and c6 are inf, a is 0. The last coefficient is then inf * 0 which equals to nan.

const double a = 1.0 / c4;

coefficients[0] = (float) (c1 * a);
coefficients[1] = (float) (c2 * a);
coefficients[2] = (float) (c3 * a);
coefficients[3] = (float) (c5 * a);
coefficients[4] = (float) (c6 * a);
2

Simple workaround should work without changing much:

if (gainFactor == 0.0)
    return makeNotch (sampleRate, frequency, Q);

Also, @IvanC is there a chance of getting more than the HP/BP/LP results of the SVF? The peak/shelving filters can be made with just an additional division or multiplication in the coefficient calculation and summing the output together. I believe that would also be an acceptable workaround for the case of G = 0.

3

we should be able to get all of these EQ types, no?
http://www.earlevel.com/main/2003/03/02/the-digital-state-variable-filter/

4

Hello guys !

I think a jassert(gainFactor > 0) would be the correct way to deal with it. For me it doesn’t make any sense to use a peak/bell filter with a gain of zero, it would be like having a commercial EQ plug-in with a gain in the range of -600 dB → +20 dB, that’s just wrong ! If someone needs an “minus infinite” gain in dB, he should just use a notch filter.

That’s not as simple as that. It is possible to get other results than LP/BP/HP with the StateVariableFilter class by doing additions and multiplications indeed. We might provide the following ones first at some point in my opinion :

  • Notch or band-reject = LP + HP
  • All-pass = LP - BP/Q + HP

But things aren’t that easy for other kinds of filters (peak + shelf). And I’m against them in StateVariableFilter for the following reasons :

  • First, the StateVariableFilter class has been designed for fast modulation purposes. Who needs fast modulation on a peak filter and why ?
  • Second, if I had to provide a peak filter there, then the class wouldn’t be called StateVariableFilter anymore, but something like TPTStructureEQ instead or something
  • Third, providing such outputs in the spirit of the original StateVariableFilter class would mean that it is possible to change at audio rate the EQ parameters without any noticeable artefact. To do so, we would need to provide three additional LinearSmoothValue objects for the gain multiplication of each output, with their values depending on the parameters. It would change a lot the processing path of the class, and so in my opinion again it would make sense only in a new class, not in StateVariableFilter.

By the way, the diagram displayed by @matkatmusic is the Chamberlin’s structure, which is not good at all in today standards because of the additional z-1 in the signal path :wink:

5

Thanks guys, I’ll add an assertion to catch that.

6

where can we read more about this? isn’t z-1 just a previously calculated output sample or input sample depending on the block diagram?

7

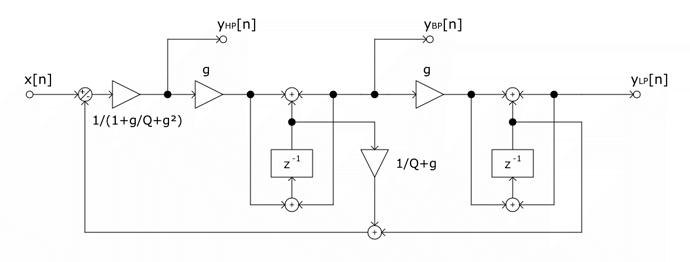
Well, the z-1 are supposed to provide a one sample delay line for getting previously calculated input/output samples as you say. However, on this specific diagram, as you can see the low pass filter signal path always gets a z-1 on its way (close to the bandpass section), which means the LP output will be delayed from the input signal.

Chamberlin’s structure back in 90s if I remember well was one of the first solutions to the audio rate modulation problem of the State Variable Filter digital simulation, but mostly a way to provide with one process call the 3/4 outputs of the SVF. The discretization is done by taking the analog block scheme, replacing the integrators with their discrete versions using Forward Euler and Backward Euler integration methods, which gives the good properties we need for fast modulation and without any z-1 appearing in a feedback loop which could be a problem. The downside is that using the Euler methods gives a bad time-invariant frequency response and even instability for given values of the resonance.

The analog block scheme :

StructureTPTContinu

Basically the structure we saw before is obtained by replacing the integrators with Euler Forward / Backward integrators :

ForwardEulerIntegrator

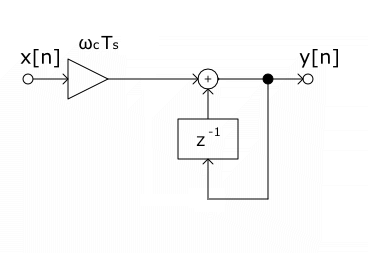
BackwardEulerIntegrator

The reason why he did that is because the standard method (seen for example in RBJ EQ Cookbook and used in juce::IIRFilter) doesn’t provide all the outputs in one go and the digital structure / topology is not the same. It uses the bilinear transform on the analog transfer function coefficients, which is equivalent to using the trapezoidal integration method on them. It is better in terms of frequency response (a lot !) even if we still have a problem there with the frequency warping of the trap method.

The RBJ EQ Cookbook result is either the DF1 or TDF2 structure below :

StructureTDF2

The thing we try to do as much as possible thanks to the “topology preserving structures” (either Chamberlin or TPT) is to never have a gain close to the output in the signal path, otherwise at that gain changes, the result might have steps or high amplitude changes in general and so audio artefacts. You can see in Chamberlin’s structure that the “f” is before the integrator so the frequency changes are smoothed. It’s not the case in the TDF2 structure where basically any change in the parameters modify the values of all the b/a gains.

One of the best solutions is to take the analog block scheme like in Chamberlin’s method, but with the integrators discretized by the trapezoidal method instead. It leads to an additional delay-free feedback loop, which can be solved analytically since everything is linear, and we get the dsp::StateVariableFilter method, described in both Vadim Zavalishin’s famous book or in Andrew Simper’s articles. We still have the frequency warping there but that’s another problem…

The trapezoidal integrator :

TPTIntegrator

The result for the SVF without the feedback loop solved analytically :

StructureTPT1
StructureTPT1.png1000Ă—380 17.2 KB

Now with the feedback loop solved (like in dsp::StateVariableFilter) :

StructureTPT3
StructureTPT3.png1000Ă—380 17.5 KB

Some bibliography :

4 Likes
8

All-pass = LP + BP + HP

To quibble a bit, that’s a peak filter in your current implementation whose gain depends on Q. You need to normalize the BP output and invert its phase to get a useful APF.

Who needs fast modulation on a peak filter and why

Asking “who needs fast modulation on _____” in the context of a synthesizer or audio plugin is kind of a bad question… I’d rather ask “who doesn’t need modulation on _____ and why?” There are a million and one reasons why you’d like the sound of a modulated peak or shelf filter in a synth or on an audio channel, from a wah to a dynamic EQ.

Second, if I had to provide a peak filter there, then the class wouldn’t be called StateVariableFilter anymore, but something like TPTStructureEQ instead or something

It’s already implicitly a TPTStructureEQ - the SVF is a single input, three output system. Right now, it’s implemented as a SISO system where there’s an implied selector switch on the outputs. You’re already implementing the system as an EQ, but only providing the three trivial shapes.

I’m all for a new class, but one of the core reasons people used the SVF in analog systems was that it allowed you to have those three outputs summed into different filter shapes. In fact, all those transfer functions in the RBJ EQ cookbook can be implemented with an SVF. I prefer using the SVF not just for it’s modulation properties, but because it’s much easier to implement analog system models using an SVF structure than messing with biquads and the bilinear transform. If you do choose to implement a new class, could you provide something like an StateVariableFilterCore that is one input - three output? I already have one of my own, but it’s not compatible with the DSP module as of yet.

9

You’re right to point that out ! It’s AP = LP - BP/Q + HP

All right :smile:

I’ll have some thoughts about it, and I’ll talk with the JUCE team about it for next iterations of the DSP module :wink:

10

JUCE V6, we presume -__-

11

Is it even worth reading the Hal Chamberlain book? Columbia University has it hosted as a pdf, if you google the full title “hal chamberlin musical applications of microprocessors”. If the information is outdated, it’s outdated. Where is a better place to start to learn about DSP for those of us without math backgrounds?

12

You can find some interesting information in that book, or in audio DSP classic books such as the DAFX one, Will Pirkle’s, or DSPGuide.com. You have tons of articles as well from conferences (AES + DAFX) or people sharing their work (Julius O Smith).

Anyway the best way to properly learn DSP is to try coding stuff by yourself from basics to more and more complex things. And improving your math skills might become essential very quickly, so you should improve that side of things as well (have a look there for that : https://minireference.com/blog/no-bs-math-and-physics-book/)

And annoucement : I’m working on some new posts on my blog about DSP in general and the DSP module. I’ll do a proper article called “IIR filters for dummies” :slight_smile:

13

And your blog is located…?

14
15

sadly last updated on January 2, 2017

16

Your answers are harsh sometimes guys :smile:

3 Likes
17

Anybody, I need this, its a pretty common thing.

18

Isn’t Peak just “LP-HP” ?

19

Isn’t Peak just “LP-HP” ?

Read starting at Section 5.3 on page 87. The RBJ Audio EQ cookbook also shows you the math but doesn’t describe it in detail.

20

I didn’t check the whole thing, and tbh some math is just to complex for me, but thats what written in the book.

Peaking filter
By subtracting the highpass signal from the lowpass signal (or also vice versa) we obtain the peaking filter

So i didn’t get why it should be complicated to create a peak filter…