Hi everyone,
In the FFT related tutorials:“Tutorial: The fast Fourier transform” and “Tutorial: Visualise the frequencies of a signal in real time”, the frequency axis(imageHeight or scopeSize) is first feeded into function f(x)=1 - exp (log (1.0- x / (imageHeight or scopeSize)) * 0.2) and then the f(x) is mapped into range (0,fftSize / 2) for transformed fft data index:fftDataIndex . What purpose is these operations?
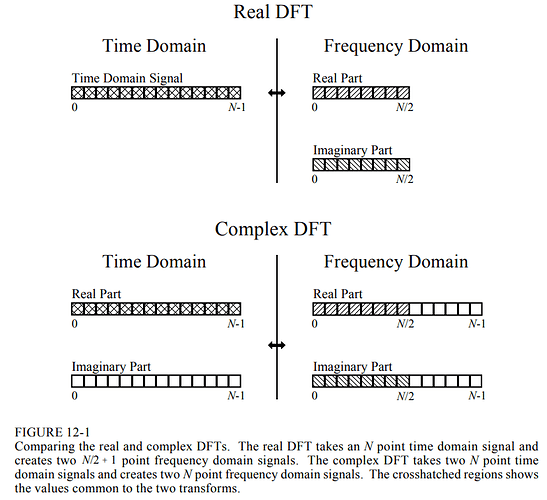
After the mapping, it seems only access the one fourth front of transformed fft frequency domain data (fftsize/2;;;;;;float fftData [2 * fftSize];). According to the instructions:http://www.dspguide.com/CH12.PDF, the transformed fft data have n+2 frequency domain data points as for n real number time domain data points.
After the function call: “performFrequencyOnlyForwardTransform (fftData)”, how the transformed n+2 fft frequency domain data points as for n real number time domain data points will be stored in the fftData array?
Given an FFT size of N, the performFrequencyOnlyForwardTransform() method requires 2N samples:
The extra N samples are for zero-padding, which effectively allows you to use a larger FFT with no extra non-zero data.
Once we’ve performed the transform, our data now contains information for frequency bins from 0Hz up to the sampling frequency mapped to the first N samples of our fftData. The resultant data however is mirrored about the Nyquist frequency - that’s just how FFT’s work - and so the only useful bins are in the range 0 to N/2.
If the data wasn’t scaled like that, half of the view would be showing just the upmost frequencies and you couldn’t see pretty much anything for frequencies below 1000Hz or so.
This is wrong. The extra memory is required because generally speaking, N complex valued time domain values will be transformed into N complex valued frequency domain values (according to the lower section of the figure of the first post).
Now if there is a real-valued input signal this is just a special case of a complex valued input signal with all imaginary values being exactly 0. So transforming N real time domain values will still lead to N complex frequency domain values. However, the resulting spectrum of real-only input data will be mirrored at N/2 so all the rest are redundant values. This is why most efficient FFT algorithms don’t compute them in the first place. However, the juce FFT wraps various more or less optimized FFT implementations and some of them will compute a simple straightforward FFT of size N which will produce N complex output values for N real valued input samples and then in a second step compute the absolute values of the first half of the output spectrum. As complex values take up twice the space of real values, it is possible that the underlying implementation will need twice the size of the input data for intermediate computation steps, so this is just for safety as you won’t know which FFT engine is chosen under the hood at runtime.
If you need zero padding as needed for convolution, you’ll need to take the next bigger FFT order and fill in the zeros by yourself, the FFT class won’t do that for you. However, in this case you’ll most likely want a complex valued output buffer anyway and will chose the performRealOnlyForwardTransform function…